Сумма внутренних углов любого выпуклого многоугольника может быть вычислена по определенной математической формуле. Рассмотрим расчет для четырнадцатиугольника (14-угольника).
Содержание
Общая формула для выпуклых многоугольников
Для любого выпуклого n-угольника сумма внутренних углов S вычисляется по формуле:
S = (n - 2) × 180°
где n - количество сторон (и углов) многоугольника.
Расчет для четырнадцатиугольника
Подставим в формулу n = 14:
| Шаг расчета | Вычисление |
| 1. Определяем количество сторон | n = 14 |
| 2. Вычисляем (n - 2) | 14 - 2 = 12 |
| 3. Умножаем на 180° | 12 × 180° = 2160° |
Итоговый результат
Сумма внутренних углов выпуклого четырнадцатиугольника равна 2160°.
Проверка правильности расчета
Для проверки можно рассмотреть несколько частных случаев:
| Многоугольник | Количество сторон (n) | Сумма углов |
| Треугольник | 3 | (3-2)×180° = 180° |
| Четырехугольник | 4 | (4-2)×180° = 360° |
| Пятиугольник | 5 | (5-2)×180° = 540° |
| Четырнадцатиугольник | 14 | (14-2)×180° = 2160° |
Вычисление величины одного угла правильного четырнадцатиугольника
Если четырнадцатиугольник правильный (все стороны и углы равны), то каждый угол можно вычислить по формуле:
α = S / n = 2160° / 14 ≈ 154,2857°
| Характеристика | Значение |
| Сумма внутренних углов | 2160° |
| Величина одного угла (правильный 14-угольник) | ≈154,2857° |
Геометрическое объяснение формулы
Формула (n-2)×180° основана на следующих принципах:
- Любой выпуклый n-угольник можно разбить на (n-2) треугольника
- Сумма углов каждого треугольника равна 180°
- Общая сумма углов многоугольника равна сумме углов всех этих треугольников
Для четырнадцатиугольника количество таких треугольников будет 14-2 = 12, следовательно, сумма углов равна 12×180° = 2160°.
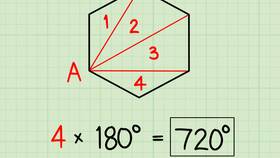
Пример разбиения
- Из одной вершины проводим диагонали ко всем несмежным вершинам
- Для 14-угольника это даст 11 диагоналей
- Диагонали разделят многоугольник на 12 треугольников
Таким образом, сумма внутренних углов выпуклого четырнадцатиугольника всегда равна 2160°, независимо от его конкретной формы, если он остается выпуклым.